数量关系：利润问题如何提高做题效率

利润问题是行测数量关系中的常考内容，可以这样说，利润问题在数量关系中，算难度稍微简单的题目，但是，利润问题也是求解比较麻烦的题目，未知量比较多，计算量比较大，是利润问题最大的难处，所以，提高利润问题的解题速度，是解决利润问题的关键，今天我们教大家一个非常好用的解题方法——特值法。

所谓特值法，就是如果题目中出现的未知量，对结果本身并没有影响的话，我们可以利用未知量的某些特性，给他赋一个便捷、简单的数值，让他在参与运算过程中，简化运算，从而方便我们求解题目要求解的未知量。接下来我们通过例题进一步体会一下。

例1

服装店买进一批童装，按每套获利50%定价卖出这批童装的80%后，按定价的八折将剩下的童装全部卖出，总利润比预期减少了390元。问服装店买进这批童装花了多少元：

A.5500

B.6000

C.6500

D.7000

【答案】C。解析：设这批童装每件的进价为x元，数量无论多少，对买进的童装的总价钱没有影响，故设数量为10件，可得下表：

根据“总利润比预期减少了390元”有，(1.5x-x)×8+(1.2x-x)×2-(1.5x-x)×10=-390，解得x=650，故买进这批童装花了650×10=6500元。本题选择C项。

例2

某商店购进一批篮球，定价为进价的125%，在售出进货量的20%后，商店决定打折促销。篮球全部卖完后，商家在该批篮球上总获利15%，问该商店这次促销价为定价的多少折：

A.8

B.8.5

C.9

D.9.5

【答案】C。解析：设进价为x，数量对于促销价为定价的多少折来说没有影响，故设销量为10，打折后促销价为y。梳理题干信息如下∶

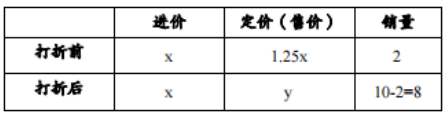
根据题意可得，(1.25x-x)×2+(y-x)×8=15%×10x，整理得y=1.125x。则该商店这次促销价为定价的1.125x÷1.25x×10=9折。本题选择C项。

例3

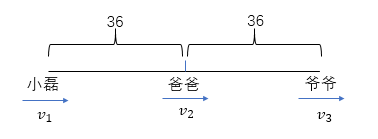
超市销售某种水果，第一天按原价售出总量的60%，第二天原价打八折售出剩下的一半，第三天按成本价全部售出。若销售全部该水果的利润率为34%，则该水果按原价销售的利润率为：

A.68%

B.51%

C.50%

D.36%

【答案】C。解析：设该水果的原价为x，成本价为y，总量为10。根据题意列表格如下：

已知销售全部该水果的利润率为 34%有，([x-y)×6+(0.8x-y)×2]÷10y×100%=34%，整理得x=1.5y，所求为(1.5y-y)÷y×100%=50%。本题选择C项。

通过以上三个例题，我们相信大家已经体会到了特值法的便捷之处，不过大家还是需要多多练习，才能真正去掌握这门方法!

易族公考永久会员

收藏 海报 链接