数量关系：工程问题

下面我们就一起来聊聊公考行测数量关系模块中相对比较简单的一个题型：工程问题。

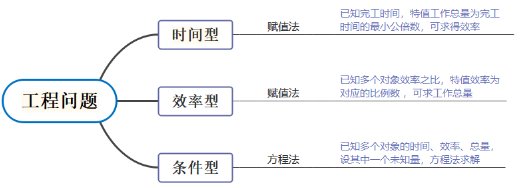
历年公考，工程问题几乎是必考题型，并且也是一个在考场上能够快速拿分，增强考生自信心的题型。一般来说，工程问题常考的有三种题型：时间类、效率类、条件类，常用的解题方法有赋值法和方程法两种。

1.时间类

时间类的工程问题一般给的条件都是某人或者某个队伍完成某项工程的时间，一般用赋值法来解题，赋工程的工作总量为题干中给定完成时间的公倍数。

【例1】一项工程，甲一人做完需30天，甲、乙合作完成需18天，乙、丙合作完成需15天，甲、乙、丙三人共同完成该工程需：( )

A.10天 B.12天

8天 D.9天

适用前提剖析：

整个题干中给出的都是完成时间，是典型的时间类工程问题，用赋值法解题。

【解析】赋工作总量为90(30、18、15的公倍数)，根据题意可知，甲的效率为3，甲乙的效率和为5，乙丙的效率和为6，则乙的效率为2，丙的效率为4，故甲乙丙的效率和为2+3+4=9，所以三人共同完成需90÷9=10(天)，因此，选择A选项。

【拓展】做题熟练的同学，其实这道题甲乙的效率这个条件可以不用，直接赋值总量30，甲的效率为1，乙丙的效率为2，然后计算即可。

2.效率类

效率类工程问题一般在题目中会给定效率之间的关系，或者通过一步简单转化找到效率之间的关系，一般解题方法是赋值效率。

【例2】某项工程如果由甲单独干6天完成总工程量的，剩余的由甲乙合作10天完成。如果此项工程由乙单独做，需要几天?

A.24 B.25

C.30 D.35

【答案】C

【解析】适用前提剖析：

整个题干中给出的量很容易求得效率比，是典型的效率类工程问题，用赋值法解题。

根据题干描述，可得甲单独6天干的量×3等于甲乙合作10天的量，如果设甲的效率为x,乙的效率为y，可得6x×3=10(x+y),整理可得8x=10y,即甲乙效率之比为5：4。

赋值甲的效率=5，乙的效率=4，则可得总的工作量=6×5×4=120，故乙单独干需要天数t=120÷4=30天。因此，选择C选项。

3.条件类

条件类工程问题一般给的条件比较多，时间、效率、总量中至少给定其中两类量，一般用方程法解题。

【例3】甲乙两个工程队共同修建一段长为2100千米的公路，甲队每天比乙队少修50千米，甲队先单独修3天，余下的路程与乙队合修6天完成，则乙队每天所修公路的长度是：

A.135千米 B.140千米

C.160千米 D.170千米

适用前提剖析：

1、整个题干中给出的具体数据，包含时间、总量以及甲乙效率之间的关系。

2、总量、时间、效率三类量都涉及到，是条件类工程问题，用方程法解题。

【解析】设乙队每天所修长度为x，则甲每天修x-50，根据题意可列式子3(x-50)+6(x+x-50)=2100，得x=170(千米)。因此，选择D选项。

通过上面几个例题，相信大家已经掌握了工程问题常见的三大题型，希望大家在自己的备考过程中能熟练应用这三种工程问题的解题技巧，相信在考场上碰到类似题目，定能如鱼得水，快人一步。

易族公考永久会员

收藏 海报 链接