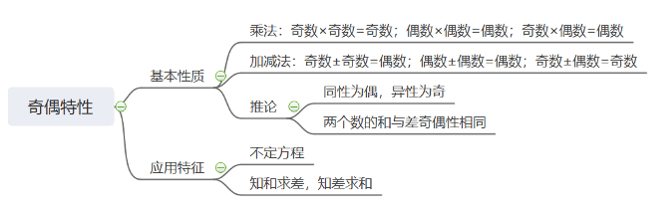
数量关系:奇偶特性
奇偶特性,具体什么是奇偶特性呢?首先我们要大家了解一下奇偶的基本法则和基本性质。这样在我们后续的解题当中才能够方便的去判定奇偶的性质。
首先是乘法运算的奇偶判定,我们来看有三个式子,第1个是奇数和奇数相乘肯定得奇数,偶数乘以偶数肯定会得到偶数,第三个奇数乘以偶数得到偶数。如果这三个式子记起来有一点麻烦,那么总结成一句话,就是在乘法运算里,有偶则偶。比如说数字相乘,只要在相乘的部分里面见到偶数了,那么整体这个乘积的结果都应该是偶数。
接下来在加减的运算中,我们也会运用到奇偶的特性。在加减法里面也是有三个式子,大家可以看一下。奇数和奇数相加减的结果是偶数,偶数和偶数相加减的结果是偶数,奇数和偶数相加减的结果是奇数。
最后除了乘法和加减法的奇偶性质,我们在这里还有两条推论,应用几率比较高的。第1条是同性为偶,异性为奇。这句话什么意思啊?它其实指的就是我们加减法上面的三个式子。我们在上面加减法的式子当中,如果是两个奇数相加或两个偶数相加,是不是一定都等于偶数?也就是说两个性质相同的数字,他们进行加减法运算,得到的都是一定是偶数。那么再看下一条,如果两个不同性质的数奇数和偶数相加减它们得到的结果是不是一定是奇数?因此推论的第1条就是总结我们加减法的。比如说x+y=15,现在我们虽然不知道x和y是奇数还是偶数,但是根据本条推论,它们的相加减结结果为15,那么x和y是否是不是一定是一个奇,一个是偶。那如果是x-y=16呢?那么我们可以确定x和y要么都是奇数,要么都是偶数。
第2个推论是,两个数的和与差奇偶性相同。这句话是这样的一个意思,比如说已知x+y=20,就能够推出x-y的结果是什么样的呢?两个数的和与差奇偶性相同,和是偶数,差就也一定是偶数。
接下来给大家说一说奇偶特性的应用。它在两种情况下进行使用。一种是在不定方程中,另一种是知合求差知差求和。比如说4x+7y=18,这是一个不定方程,我们除了用代入排除法解决以外,也可以考虑它的奇偶特性。大家看,和为18是一个偶数,4x和7y,哪一个是我们能确定的?乘法当中有偶则偶因此4x一定是一个偶数。什么样的数相加可以得到偶数同性相加是吧?那4x是偶数,7y也一定就是偶数了,也就是说y也一定是偶数,得到这样的结论,我们在题目当中可能选项就能排除选掉一半了,难度也就直接变低了。
那第2个应用知和求差知差求和是什么意思呢?比如说我们求x-y=多少,已知x+y=17。之和就是知道它的和求差,求它的差。具体是多少我不知道,但是我能判定出来两个数的和是奇数,和与差奇偶性相同,因此它们的差也是奇数。如果选项当中只有一个奇数,就可以迅速选出来。这就是奇偶特性的两种应用。
这就是奇偶特性的性质以及应用的条件。接下来我们一起来看例题。
例:方程px+q=99的解为x=1,p、q均为质数,则求p×q的值。
A、194
B、197
C、135
D、155
第1句话我们知道这个等式的解是x=1,也就是说把x等于1代入到方程当中,这个等式是成立的。所以我把x=1代入就得到一个式子,得到p+q=99,现在我们要求什么呀?p×q=多少?有同学问老师这怎么求呀,我好像看不出来,那这道题我们来看知和求差用得上吗?我们知道和,但不是求差是求积,求不出来。这也算一个不定方程,两个未知数,一个式子我们试试看能不能用奇偶特性来解决。我们先确定一件事,两个数相加等于99,是一个奇数,那么p和q是不是一个奇,一个是偶。回忆下我们的推论第1条,是不是异性相加减结果为奇数啊?那我们一起想一想,既然p、q一个是奇数,一个是偶数,那么一个奇数和一个偶数相乘的结果应该是什么?是不是一定是一个偶数啊,观察选项,发现只有一个选项能满足了,只有A选项是偶数。所以本题答案选择的是A项,这就可以了。
有的同学会问,如果答案当中不止一个偶数呢,我们也可以继续往下去算。上节课给大家说到质数,是不是说质数当中只有一个偶数就是2。两个质数相加等于99,也就是一奇一偶的质数相加,其中一定有一个是2,那另外一个就是97。我们算他们的成绩就可以了,2×97=194选择A选项。
最后,我们来总结一下吧
声明:
1、本站部分资源来自于网络,如您在访问的过程中发现本站内容侵犯了原著者的合法权益或内容有不妥之处,可发送邮件至“cloud20150618@qq.com”或者在右侧扫码添加管理员微信进行处理。
2、如遇本站资源无法下载、无法查看,或者其他任何问题,请及时联系我们,我们将第一时间修复。