数量关系:不定方程组问题
北魏时期,我国出现了一位伟大的数学家张邱建,他从小聪明好学,酷爱算术。在日常生活中,遇到计算方面的难题,别人不会,他却能解决,因此从小就被称为神童。当地的县令为了考验他,给他出了一个难题:“鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一;百钱买百鸡,则翁,母,雏各几何?”,这就是《张邱建算经》中记录的著名的百钱买百鸡问题,这也是世界上首次提出三元一次不定方程组及其一种解法,领先欧洲一千多年。在古代没有不定方程组的情况下,这可是一道难题了,但学习了不定方程组以后,这将是一个非常简单的问题。那么接下来我们一起来学习关于不定方程(组)的相关知识点。


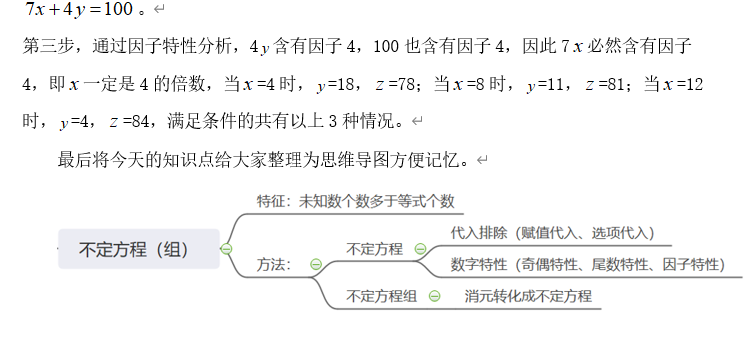
奇偶特性:加减法(奇反偶同,结果为奇数,证明两个加数奇偶性相反;结果为偶数,证明两个加数奇偶性相同)、乘法(有偶则偶)。
余数特性:余数的可加性、可减性、可乘性。
尾数特性:当方程中某项出现尾数0或5的时候考虑使用。
2.不定方程组:消元后转化为不定方程求解即可。
接下来我们看几个例题巩固一下:
例1.(2015 江苏)设a、b均为正整数,若11a+7b=84,则a的值为:
A. 4
B. 5
C. 7
D. 8
解析:根据因子特性,7b含有因子7,84含有因子7,11a必然含有因子7,因此a必然是7的倍数,选择C。
例2.(2019 湖北)某足球比赛售出40元、80元、120元门票共2000张,其中80元的门票数是120元的门票数的2倍,比赛门票收入共12万元。则40元门票售出多少张?
A.1000
B.1150
C.1200
D.1250
解析:设120元的门票为x张,则80元的为2x张,设40元的为y张,根据总和为2000可得3x+y=2000,根据余数的可加性,3x除以3余0,2000除以3余2,可得y除以3必余2,因此选择D选项。

声明:
1、本站部分资源来自于网络,如您在访问的过程中发现本站内容侵犯了原著者的合法权益或内容有不妥之处,可发送邮件至“cloud20150618@qq.com”或者在右侧扫码添加管理员微信进行处理。
2、如遇本站资源无法下载、无法查看,或者其他任何问题,请及时联系我们,我们将第一时间修复。