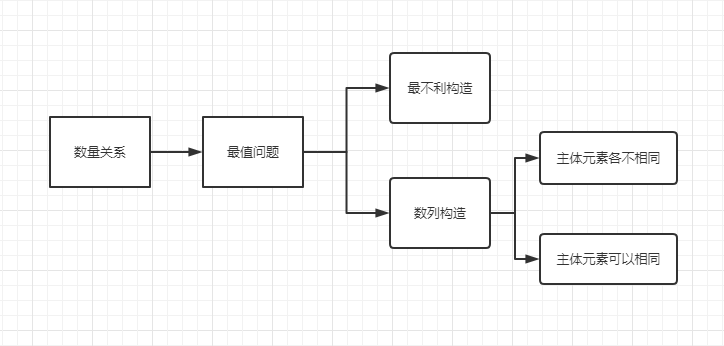
数量关系:常见失误题之数列构造
今天,老师就带着大家一起来看一下在数量关系当中。一个比较常见的陷阱题型——数列构造题。可能很多同学就会说了数列构造还不简单吗?直接用兔兔老师教的,排序-定位-构造-求和4个步骤解出来就可以啦!诚然针对于一般的题目,只需要按照这几个步骤就可以了,列构造的相应题目特征是“排名第几的……最多(少)……并且每一个主体分得到的元素各不相同”,例如:
现有21本故事书要分给5个人阅读,如果每个人得到的数量均不相同,那么得到故事书数量最多的人至少可以得到( )本。
A. 5
B. 7
C. 9
D. 11
【解析】第一步,本题考查最值问题。
第二步,设得到故事书数量最多的人得到 x 本,由于每个人得到的故事书数量各不相同,则其余 4 人得到的故事书依次为(x-1)、 (x-2)、(x-3)、(x-4)时 x 取最小值,可列方程 x+(x-1)+(x-2)+(x-3)+(x-4)=21,解得 x=6.2,即得到故事书数量最多的人至少可以得到 7 本。 因此,选择 B 选项。
但是啊,还有另外的一种题型,他没有“主体分得的元素各不相同”这句话,那么我们在做题的时候,如果没有注意到这句话的话,就可能在构造的步骤当中啊,其实余下的那些主体数据可以是一样的,但是往往我们就忽略掉了,依旧按照惯性思维觉得其余主体分配的数量各不相同,那可能得到的就不是我们想要的正确答案或者浪费了大量的时间了,例如:
某高校计划招聘81名博士,拟分配到13个不同的院系,假定院系A分得的博士人数比其他院系都多,那么院系A分得的博士人数至少有多少名?
A. 6
B. 7
C. 8
D. 9
【解析】第一步,本题考查最值问题中的数列构造问题。
第二步,总共招聘 81 名博士,要想院系 A 分得的博士数最少,则应构造其余院系分得的博士数尽可能多。设院系 A 分得博士 x 名,那么其余 12 个院系最多均有 x-1 名,可列方 程:x+(x-1)×12=81,解得 x≈7.2,那么院系 A 分得的博士至少有 8 名。 因此,选择 C 选项。
在做这道题构造数列的过程当中可能有一部分同学就会以一种惯性思维,觉得院系A分到了X名博士,那么分配到博士第二多的院系就得到(X-1)名,第三多就分配(X-2)名……最终导致解出来的答案错误,然后回到选项当中发现没有对应答案,再来回过头来看题做题,大量的时间就在这个地方被浪费掉了,所以我们在审题的时候,就一定要仔细分清楚,这种题应该怎么做。
好啦,这就是今天老师在数量关系题目当中给大家的分享啦,你学会了吗?
声明:
1、本站部分资源来自于网络,如您在访问的过程中发现本站内容侵犯了原著者的合法权益或内容有不妥之处,可发送邮件至“cloud20150618@qq.com”或者在右侧扫码添加管理员微信进行处理。
2、如遇本站资源无法下载、无法查看,或者其他任何问题,请及时联系我们,我们将第一时间修复。