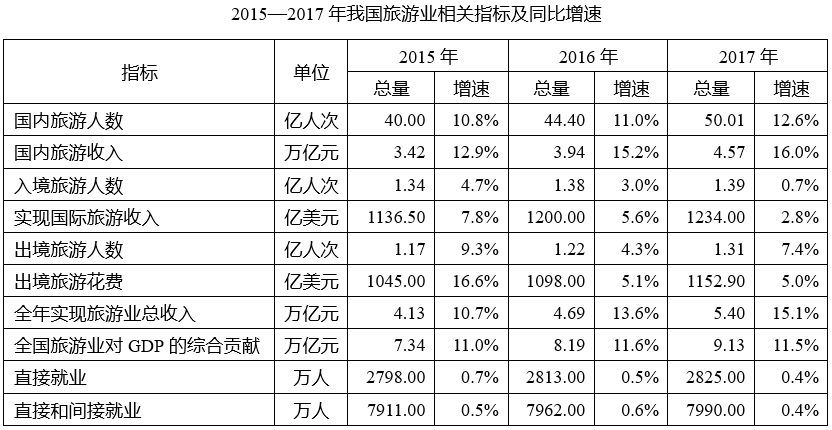
资料分析：基期平均数计算

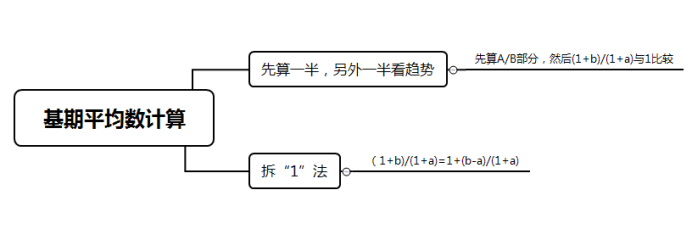
平均数相关是资料分析中较为重要的题型之一，一般包含六个常见考点：一是现期平均数计算，即平均数的基础计算;二是现期平均数大小比较，属于简单的分数比较类;三是基期平均数计算，其公式为，一般计算量相对比较大，但是可以采用先算一半、另外一半看趋势或者拆1法等方法进行速算;四是两期平均数比较，有对应的快速判定口诀，即只需比较分子增长率a和分母增长率b的大小即可;五是平均数的增长量，即现期平均数和基期平均数的差值，其公式为;六是平均数的增长率，也称均值增长率，其公式为。在这六种考查题型中，基期平均数的计算量相对比较大，也是速算技巧应用最为灵活的一种题型。

基期平均数计算，是资料分析中较为复杂的一种计算，有人也称其为重叠分数计算。如果总量为A，增长率为a;总份数为B，增长率为b，则现期平均数为，而基期平均数的计算公式为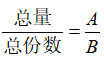：，明显发现这是一个复杂的式子，所以在实际做题过程中，一定要采取相应的速算技巧，才会变得比较简单。下面，我们通过一个具体的例子来看看基期平均数计算这个复杂公式的基本应用：

【例1】2015年2月，我国快递业务量完成8.2亿件;同比增长18.7%;业务收入完成136.0亿元，同比增长22.5%。

2014年2月，平均每笔快递业务的收入在以下哪个范围之内?

A. 16.07 B. 16.87

C. 17.28 D. 18.29

【答案】A

【解析】第一步，识别题型，本题考查基期平均数计算。

第二步，定位文字材料中的数据：2015年2月，我国快递业务量完成8.2亿件，同比增长18.7%;业务收入完成136.0亿元，同比增长22.5%。

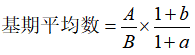
第三步，根据基期平均数计算公式，则2014年2月平均每笔快递业务的收入(元)。

因此，选择A选项。

不难发现，在实际计算的过程中可以将基期平均数这个复杂的公式进行拆分，一般先计算现期平均数的部分，然后另外一部分可以通过分子与分母的大小来判定这个式子是比1大还是比1小，最后再将两个式子进行整合，看其值的变化趋势，从而得到最终的结果。除了这种计算方法以外，基期平均数计算有时候还有一些变形的简化计算方式，即将其中这个部分，变形为，来达到简化计算的目的，又称为“拆1法”。下面，我们继续通过一个具体的例子来看看“拆1法”的基本应用：

【例2】2014年，东部地区商品房销售面积54756万平方米，比上年下降13.7%，降幅比1—11月份收窄1.3个百分点;销售额43607亿元，下降11.6%，降幅收窄2.1个百分点。中部地区商品房销售面积33824万平方米，下降3.9%，降幅收窄0.4个百分点;销售额16558亿元，增长0.2%，1—11月份为下降0.9%。西部地区商品房销售面积32068万平方米，增长0.6%，增速回落0.6个百分点;销售额16127亿元，增长3.5%，增速回落0.6个百分点。

2013年西部地区商品房销售价格为：

A. 3694元/平方米 B. 4674元/平方米

C. 4888元/平方米 D. 5008元/平方米

【答案】C

【解析】第一步，识别题型，本题考查基期平均数计算。

第二步，定位文字材料可知，“2014年，西部地区商品房销售面积32068万平方米，增长0.6%;销售额16127亿元，增长3.5%”。

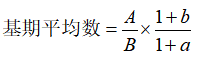
第三步，先统一单位，32068万平方米=3.2068亿平方米，然后再根据基期平均数计算公式，可得2013年西部地区商品房销售价格(元/平方米)，与 C 选项最接近。

因此，选择C 选项。

以上就是基期平均数中最为常见的两种速算方法，虽然称作速算，但一些最基础的四则运算还是要有所涉及的。相比较而言，只要掌握了一定的速算技巧，然后再结合基期平均数公式本身的拆分变形，一般可能不需要很复杂的计算就可以轻松得到答案。当然，考生在处理这种复杂计算的时候，还要注意答案的精准度，要结合已知条件和最终的选项来找准做题方法，否则就容易出错。

易族公考永久会员

收藏 海报 链接