判断推理:分析推理之六面体中的移面大
判断推理当中的六面体问题是不少考生心中的“老大难”,对于空间想象能力较差的人来说做起来着实难度不小,不少考生绞尽脑汁,发明出了“橡皮法”、“折纸法”。虽然大部分省份对于能否用橡皮解题没有明确规定,但行测科目时间紧张,无论是折纸还是画橡皮消耗的时间都很多,所以即便是能选出正确答案性价比也不高。因此,掌握六面体的解题方法能够帮助我们又快又准的选出正确答案。
基于六面体面与面之间的关系,解决六面体问题的方法主要分为两种:相对面排除法和相邻面排除法。其中,能够适用相对面排除法的题目并不多,所以一般我们解决六面体问题所采用的方法都是相邻面法。但做题过程中我们发现,出题人为了保证六面体题目的难度,题干立体图形当中的相邻面在展开图中并不“相邻“。例如下面这道例题:
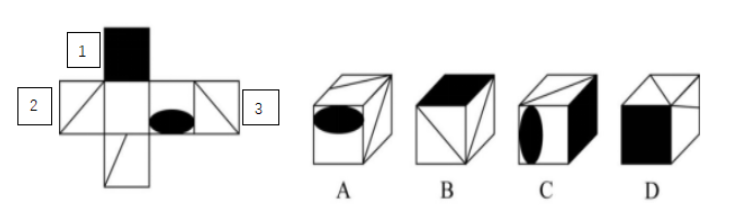
以B选项为例,B项立体图形中展示的相邻面在展开图当中分别标记为1、2、3号,但这三个面在展开图当中并不相邻,因此要想直接验证B项正确与否需要非常强的空间想象能力。
那么有没有一种方法能够将这三个面移动到一起,在展开图当中也呈现相邻的状态呢?这就是要跟大家分享的“移面大法”。
什么是“移面大法”?我们知道,同一个立方体有11种不同的展开方式,我们选择其中一种展开:
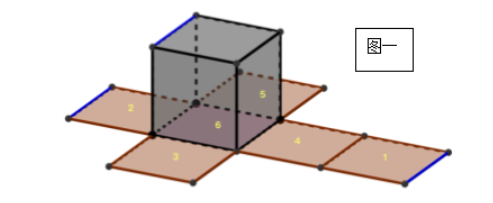
上图是从蓝色楞作为起点,将六面体展开所形成的展开图,展开图中的蓝色边是折成立体图时两个面的公共边。当然,我们也可以再换一种展开方式,比如下图这种从红色楞作为起点的展开方式:
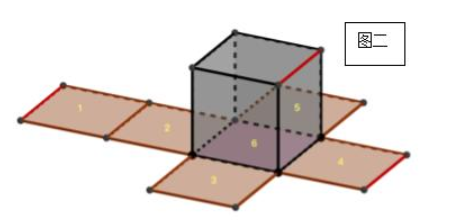
这两个展开图是同一六面体的不同展开方式,对比两图你会发现,1号面在图一中位于4号面的右侧,但在图二中却出现在了2号面的左侧,看上去好像1号面进行“平移”了一样。这就是“移面大法”的第一种移动方式:四面相邻时,最边缘的面可以另一个边缘平移,折成的六面体不变。
再换一种展开方式,如下图:
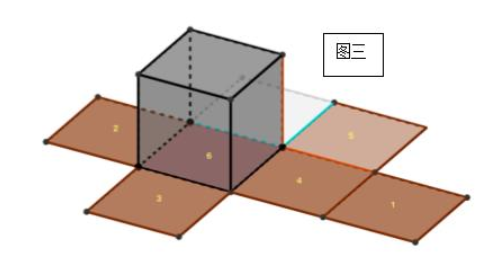
5号面在图一中位于6号面上面,而且两面的公共边在图三中已用蓝色笔标出,而在图三中,5号面出现在了4号面上面,公共边用红色笔标出。这两个展开图也是同一六面体的不同展开方式,对比两图,看上去好像是5号面从图一中原来的位置“旋转”到图三中的位置一样。这就是“移面大法”第二种移动方式:垂直边的两个面将其中一个旋转90°,折成的六面体不变。
以上两种移面方式就是解六面体常用的“移面法”,通过移面,可以进一步使用箭头法、公共边公共点法验证选项。比如,仍以上面的例题为例:
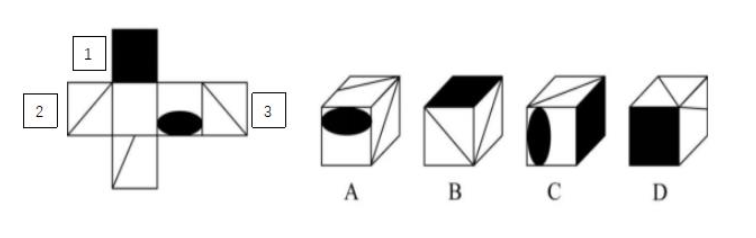
B项中的三个面并不相邻,我们可以通过移面使他们在展开图中变成相邻的面:将1号面进行旋转、2号面进行平移,最终得到的展开图如下图:
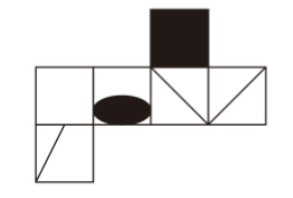
此时,再通过箭头法就能很轻松的判断出B项能由该展开图折叠而成,其他选项留给读者自行验证。
声明:
1、本站部分资源来自于网络,如您在访问的过程中发现本站内容侵犯了原著者的合法权益或内容有不妥之处,可发送邮件至“cloud20150618@qq.com”或者在右侧扫码添加管理员微信进行处理。
2、如遇本站资源无法下载、无法查看,或者其他任何问题,请及时联系我们,我们将第一时间修复。